Hubungan Sudut Pusat Dengan Panjang Busur Lingkaran
Sebelum Anda mempelajari bagaimana hubungan sudut pusat lingkaran dengan panjang busur lingkaran, Anda harus mengerti terlebih dahulu apa itu sudut pusat lingkaran dan apa itu panjang busur lingkaran. Sudut pusat dan panjang busur lingkaran merupakan unsur-unsur atau bagian-bagian dari lingkaran yang sangat penting anda ketahui.
Satu hal lagi yang Anda perlu ingat agar mudah
memperlajari hubungan antara sudut pusat dengan panjang busur lingkaran yaitu cara mencari keliling lingkaran dan konsep perbandingan senilai atau seharga. Apa
hubungannya perbandingan senilai dengan materi ini? Oke nanti akan dijelaskan
secara mendetail. Sekarang perhatikan gambar di bawah ini!
Pada gambar di atas sebuah lingkaran dengan
jari-jari r memiliki sudut pusat AOB
yang besarnya α (α baca: alfa) dan memiliki panjang busur garis lengukung AB.
Kemudian apa yang terjadi jika sudut α diperbesar menjadi sudut β (β baca
betta) seperti gambar di bawah ini?
Ternyata panjang busur lingkaran menjadi besar setelah sudut pusatnya diperbesar. Nah inilah yang disebut dengan perbandingan senilai atau seharga. Di mana semakin besar sudut pusat maka semakin besar panjang busurnya, begitu juga sebaliknya semakin kecil sudut pusatnya maka semakain kecil panjang busurnya. Sekarang bagaimana kalau sudut α tersebut diubah menjadi satu lingkaran penuh (360°)?
Ternyata setelah sudut pusat diubah menjadi satu
lingkaran penuh (360°) maka panjang busur lingkaran menjadi keliling lingkaran.
Nah dari pernyataan tersebut dapat diperoleh hubungan antara sudut pusat,
panjang busur dengan keliling lingkaran yaitu panjang busur per keliling
lingkaran sama dengan besarnya sudut pusat per sudut satu lingkaran penuh (360°).
Secara matematis pernyataan tersebut dapat dirumuskan:
Panjang
busur/keliling = sudut pusat/360°
Contoh soal:
Perhatikan gambar berikut.
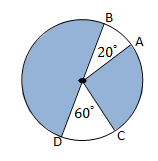
Jika panjang busur AB = 45 cm, maka berapakah panjang busur CD?
Penyelesaian:
Hubungan Sudut Pusat dengan Sudut Keliling
Sudut pusat adalah sudut yang dibatasi oleh dua jari-jari lingkaran dan titik sudutnya merupakan titik pusat lingkaran
Sudut keliling adalah sudut yang dibatasi oleh dua talibusur dan titik sudutnya terletak pada keliling tepi lingkaran.
Perhatikan gambar diatas, ∠AOC dinamakan dengan sudut pusat, dan ∠ABC dinamakan dengan sudut keliling.
Pada gambar berikut ini, ∠AOC adalah sudut pusat dan ∠ABC adalah sudut keliling dimana keduanya menghadap busur AC.
Ketika sudut pusat dan sudut
keliling menghadap busur yang sama, maka besar sudut pusat adalah dua
kali dari besar sudut keliling.
BESAR SUDUT KELILING YANG MENGHADAP DIAMETER LINGKARAN Perhatikan gambar berikut ini.
Sudut pusat AOB menghadap busur AB(besar ∠AOB = 180°,
karena merupakan setengah lingkaran). Perhatikan juga bahwa sudut
keliling ACB juga menghadap busur AB, sehingga berdasarkan hubungan
antara sudut pusat dan sudut keliling diperoleh:
Sudut pusat = 2 × sudut keliling
∠AOB = 2 ×∠ACB
180° = 2 ×∠ACB
∠ACB = 1/2 × 180° = 90°
Maka dapat disimpulkan:
Sudut pusat = 2 × sudut keliling
Sudut keliling = ½ sudut pusat
BESAR SUDUT KELILING YANG MENGHADAP DIAMETER LINGKARAN Perhatikan gambar berikut ini.
Sudut keliling yang menghadap diameter lingkaran besarnya 90° (sudut siku-siku)
SUDUT-SUDUT KELILING YANG MENGHADAP BUSUR YANG SAMA
Jadi besar ∠ACB=∠ADB=∠AEB
Sudut-sudut keliling yang menghadap busur yang sama adalah sama besar
