Contoh Soal Lingkaran

Lihat Disini

Hubungan Sudut Pusat dengan Panjang Busur dan Keliling Lingkaran

Hubungan Sudut Pusat Dengan Panjang Busur Lingkaran

Sebelum Anda mempelajari bagaimana hubungan sudut pusat lingkaran dengan panjang busur lingkaran, Anda harus mengerti terlebih dahulu apa itu sudut pusat lingkaran dan apa itu panjang busur lingkaran. Sudut pusat dan panjang busur lingkaran merupakan unsur-unsur atau bagian-bagian dari lingkaran yang sangat penting anda ketahui.  

Satu hal lagi yang Anda perlu ingat agar mudah memperlajari hubungan antara sudut pusat dengan panjang busur lingkaran yaitu cara mencari keliling lingkaran dan konsep perbandingan senilai atau seharga. Apa hubungannya perbandingan senilai dengan materi ini? Oke nanti akan dijelaskan secara mendetail. Sekarang perhatikan gambar di bawah ini!

Pada gambar di atas sebuah lingkaran dengan jari-jari r memiliki sudut pusat AOB yang besarnya α (α baca: alfa) dan memiliki panjang busur garis lengukung AB. Kemudian apa yang terjadi jika sudut α diperbesar menjadi sudut β (β baca betta) seperti gambar di bawah ini?

Ternyata panjang busur lingkaran menjadi besar setelah sudut pusatnya diperbesar. Nah inilah yang disebut dengan perbandingan senilai atau seharga. Di mana semakin besar sudut pusat maka semakin besar panjang busurnya, begitu juga sebaliknya semakin kecil sudut pusatnya maka semakain kecil panjang busurnya. Sekarang bagaimana kalau sudut α tersebut diubah menjadi satu lingkaran penuh (360°)?

Ternyata setelah sudut pusat diubah menjadi satu lingkaran penuh (360°) maka panjang busur lingkaran menjadi keliling lingkaran. Nah dari pernyataan tersebut dapat diperoleh hubungan antara sudut pusat, panjang busur dengan keliling lingkaran yaitu panjang busur per keliling lingkaran sama dengan besarnya sudut pusat per sudut satu lingkaran penuh (360°). Secara matematis pernyataan tersebut dapat dirumuskan:

Panjang busur/keliling =  sudut pusat/360°

Contoh soal:

Perhatikan gambar berikut.

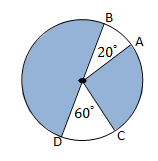
Jika panjang busur AB = 45 cm, maka berapakah panjang busur CD?

Penyelesaian:

 Hubungan Sudut Pusat dengan Sudut Keliling

Sudut pusat adalah sudut yang dibatasi oleh dua jari-jari lingkaran dan titik sudutnya merupakan titik pusat lingkaran
Sudut keliling adalah sudut yang dibatasi oleh dua talibusur dan titik sudutnya terletak pada keliling tepi lingkaran.

Perhatikan gambar diatas, ∠AOC dinamakan dengan sudut pusat, dan ∠ABC dinamakan dengan sudut keliling.

Pada gambar berikut ini, ∠AOC adalah sudut pusat dan ∠ABC adalah sudut keliling dimana keduanya menghadap busur AC.

Ketika sudut pusat dan sudut keliling menghadap busur yang sama, maka besar sudut pusat adalah dua kali dari besar sudut keliling.

Sudut pusat = 2 × sudut keliling Sudut keliling = ½ sudut pusat

BESAR SUDUT KELILING YANG MENGHADAP DIAMETER LINGKARAN Perhatikan gambar berikut ini.

Sudut pusat AOB menghadap busur AB(besar ∠AOB = 180°, karena merupakan setengah lingkaran). Perhatikan juga bahwa sudut keliling ACB juga menghadap busur AB, sehingga berdasarkan hubungan antara sudut pusat dan sudut keliling diperoleh: Sudut pusat = 2 × sudut keliling ∠AOB = 2 ×∠ACB  180° = 2 ×∠ACB  ∠ACB = 1/2 × 180° = 90°  Maka dapat disimpulkan:

Sudut keliling yang menghadap diameter lingkaran besarnya 90° (sudut siku-siku)

SUDUT-SUDUT KELILING YANG MENGHADAP BUSUR YANG SAMA

∠ACB,∠ADB,dan ∠AEB adalah sudut-sudut keliling yang menghadap busur yang sama yaitu busur AB. ∠AOB adalah sudut pusat yang juga menghadap busur AB. Berdasarkan hubungan sudut pusat dan sudut keliling yaitu: Sudut keliling = ½ sudut pusat Maka: ∠ACB = 1/2 × ∠AOB  ∠ADB = 1/2 × ∠AOB 

∠ACB,∠ADB,dan ∠AEB adalah sudut-sudut keliling yang menghadap busur yang sama yaitu busur AB. ∠AOB adalah sudut pusat yang juga menghadap busur AB. Berdasarkan hubungan sudut pusat dan sudut keliling yaitu: Sudut keliling = ½ sudut pusat Maka: ∠ACB = 1/2 × ∠AOB  ∠ADB = 1/2 × ∠AOB  ∠AEB = 1/2 × ∠AOB 
Jadi besar ∠ACB=∠ADB=∠AEB 

Sudut-sudut keliling yang menghadap busur yang sama adalah sama besar

Sumber:
http://mafia.mafiaol.com/2014/02/hubungan-sudut-pusat-panjang-busur.html

http://www.danlajanto.com/2016/01/soal-dan-pembahasan-hubungan-sudut.html 

http://www.jendelailmu.net/2016/03/sudut-pusat-sudut-keliling-lingkaran.html 

Keliling dan Luas Lingkaran

Hubungan antara Keliling dan Luas Lingkaran 

Untuk memahami hubungan antara keliling dengan luas lingkaran Anda harus paham dengan konsep keliling lingkaran dan luas lingkaran. Hubungan antara keliling dengan luas lingkaran cocok digunakan untuk menjawab soal-soal ulangan umum dan ujian nasional yang bentuk soalnya berupa pilihan ganda karena membutuhkan waktu yang singkat.

Jika Anda mampu menguasai materi tentang hubungan keliling lingkaran dengan luasnya, Anda tidak perlu mencari jari-jari atau diameternya jika yang diketahui keliling atau luasnya saja. Bagaimana caranya? Sekarang coba simak baik-baik pembahasan berikut ini.

Kita gunakan rumus keliling lingkaran dengan mencari jari-jarinya, misalkan keliling lingkaran K dan luasnya L, maka:

K = 2πr => r = K/2π

Sekarang substitusi persamaan jari-jari r ke rumus luas lingkaran, maka:

L = πr²

L = π(K/2π)²

L = π.K²/4π²

L = K²/4π

Dari persamaan hubungan antara keliling lingkaran dengan luasnya juga bisa dicari hubungan kebalikannya yaitu hubungan antara luas lingkaran dengan kelilingnya, yakni:

L = K²/4π

K² = 4πL

K = √(4πL)

Sekarang coba perhatikan contoh soal berikut ini tentang hubungan keliling lingkaran dengan luasny atau sebaliknya.

Cara Menghitung Perubahan Luas dan Keliling Jika Jari-jari berubah 

Misalkan sebuah lingkaran memiliki jari-jari r1 akan diperbesar sehingga jari-jarinya menjadi r2 dimana r2 > r1. Jika luas lingkaran semula adalah L1 serta luas lingkaran setelah mengalami perubahan jari-jari adalah L2 maka selisih luas kedua lingkaran tersebut adalah sebagai berikut.
L2 – L1 = πr2² – πr1²
L2 – L1 = π (r2² – r1²)
L2 – L1 = π (r2 – r1) (r2+r1)
Apabila keliling lingkaran semula adalah K1 selanjutnya keliling setelah mengalami perubahan jari-jari adalah K2 maka selisih keliling kedua lingkaran adalah sebagai berikut.
K2 – K1 = 2πr2 – 2πr1
K2 – K1 = 2π (r2 – r1)
Kita juga dapat menghitung perbandingan luas serta keliling limgkaran jika besarnya jari-jari berubah.
Perbandingan luas kedua lingkaran tersebut yaitu sebagai berikut.
L2 : L1 = πr2² : πr1²
L2 : L1 = r2² : r1²
selanjutnya perbandingan kelilingnya yaitu sebagai berikut.
K2 : K1 = 2πr2 : 2πr1
K2 : K1 = r2 : r1
Berdasarkan uraian tersebut kita dapat simpulkan bahwa lingkaran yang berjari-jari r1, setelah mengalami perubahan jari-jari menjadi r2 dimana r2>r1 maka selisih dan perbandingan luas serta kelilingnya sebagai berikut.

L2 – L1 = π (r2 – r1) (r2 + r1)

K2 – K1 = 2π (r2 – r1)

L2 : L1 = r2² : r1²

K2 : K1 = r2 : r1

Perhatikan contoh soal berikut.
Hitunglah selilih serta perbandingan luas serta keliling lingkaran yang berjari-jari 4cm dan 6cm?
Penyelesaian :
Diketahui :
r1 = 4cm
r2 = 6cm
Ditanya : perbandingan serta selisih luas dan kelilingnya?
Jawab :
Selilih Luas 
L2 – L1 = π (r2 – r1 ) (r2 + r1)
L2 – L1 = π (6 – 4) (6 + 4)
L2 – L1 = π × 2 × 10
L2 – L1 = 20π cm²
Selisih keliling
K2 – K1 = 2π (r2 – r1)
K2 – K1 = 2π (6 – 4)
K2 – K1 = 2π (2)
K2 – K1 = 4π cm
Perbandingan luas
L2 : L1 = r2² : r1²
L2 : L1 = 6² : 4²
L2 : L1 = 36 : 16
L2 : L1 = 9 : 4
Perbandingan keliling
K2 : K1 = r2 : r1
K2 : K1 = 6 : 4
K2 : K1 = 3 : 2

Hubungan antara Sudut Pusat, Panjang Busur, dan Luas Juring

Hubungan Sudut Pusat, Panjang Busur, dan Luas Juring

Sudut pusat adalah sudut yang dibentuk oleh dua jari-jari yang berpotongan pada pusat lingkaran. Pada gambar di samping, ˂AOB = α adalah sudut pusat lingkaran. Garis lengkung AB disebut busur AB dan daerah yang diraster (diarsir) disebut juring.

 

Hubungan antara sudut pusat, panjang busur, dan luas juring adalah sebagai berikut.

Sekarang perhatikan Gambar di atas tersebut. Dari gambar tersebut diperoleh

Sekarang, misalkan ∠ COD = satu putaran penuh = 360° maka keliling lingkaran = 2πr, dan luas lingkaran = πr² dengan r jari-jari, akan tampak seperti Gambar di atas, sehingga diperoleh

Dengan demikian, diperoleh rumus panjang busur AB, luas juring AB, dan luas tembereng AB pada Gambar di atas adalah

panjang busur AB = (α : 360°) x 2πr

luas juring OAB = (α : 360°) x πr²

luas tembereng AB = luas juring OAB – luas Δ AOB.

Contoh Soal Tentang Hubungan Antara Sudut Pusat, Panjang Busur, Dan Luas Juring

Perhatikan Gambar di atas. Diketahui panjang jari-jari OA = 28 cm. Jika besar ∠ AOB = 90°, hitunglah

1. panjang AB ;
2. luas juring OAB;
3. luas tembereng AB.

Penyelesaian: 

1. Panjang AB = (∠ AOB : 360°)  x 2πr 

    Panjang AB = (90°: 360°)  x 2 x 22/7 x 28 cm 

    Panjang AB = (1/4)  x 2 x 22/7 x 28 cm 

    Panjang AB =  44 cm 

2. Luas juring OAB = (∠ AOB : 360°)  x πr2 

     Luas juring OAB = (90° : 360°)  x 22/7 x (28 cm)2 

     Luas juring OAB = (1/4)  x 22/7 x 28 x 28 cm² 

     Luas juring OAB = 616 cm² 

3. Karena besar sudut AOB = 90°, maka Δ AOB adalah Δ siku-siku sisi 10 cm, sehingga 

Luas Δ AOB = ½ alas x tinggi 

Luas Δ AOB = ½ x 28 cm x 28 cm 

Luas Δ AOB = 392 cm2

^{Luas tembereng AB = luas juring AOB – luas ΔAOB}   

Luas tembereng AB = 616 cm² – 392 cm2 

Luas tembereng AB = 224 cm² 

 

Menggunakan Hubungan Sudut Pusat, Panjang Busur, Luas Juring dalam Kehidupan Sehari-hari

 

Contoh :

1.

Sebuah roda mempunyai 8 jeruji dengan jari-jari 28cm. Besar sudut roda 360^◦. Tentukan:

a       a. Besar sudut antar jeruji (α)

  b. Panjang busur AB 

Pembahasan:

            Diketahui:      r = 28 cm

                                    Besar sudut roda = 360^◦

            Ditanya:         a. α

                                    b. panjang busur AB

            Jawab:           a. Keliling      =   2ᴫr

                                                          =    2 x 22/7 x 28 cm

                                                          =    176 cm 

                                           α   = 360° : jumlah jeruji

                                                = 360° : 8

                                                                             =  45°

b.  α : 360°   = panjang busur AB : keliling lingkaran

     45° : 360°= panjang busur AB : 176 cm

     1 : 8          = panjang busur AB : 176 cm

    panjang busur AB = 176 cm : 8

    panjang busur AB = 22 cm

 

2. 

 

 

Sebuah pizza dipotong menjadi 6 bagian. Sudut setiap potong pizza sebesar 60^◦. Panjang busur PQ sebesar 22 cm. 

Hitunglah :

a. r

b. luas per potong pizza

Pembahasan:

Diketahui:      Jumlah potongan pizza = 6 bagian

                        α = 60^o

                        Panjang busur PQ = 22 cm

Ditanya:        a. r

                       b. luas per potong pizza

Jawab:          a.          α : 360°    = panjang busur PQ : keliling lingkaran

 60° : 360°= 22 cm : keliling lingkaran

  1 : 6        = 22 cm :  keliling lingkaran

  keliling lingkaran = 22 cm x 6

                                     keliling lingkaran = 132 cm 

                                     keliling lingkaran = 2ᴫr

      132 cm          = 2 x 22/7x r

        r                    = (132 cm x 7) : 44 cm

        r                    = 924 cm : 44 cm

            r                    = 21 cm

b.         Luas lingkaran         = ᴫr²

                                          = 22/7 x (21 cm)²

                                                                                 = 22/7 x 441 cm²                                                                                  = 1386 cm²

                                 α : 360°      = luas per potong pizza : luas lingkaran

                                  60° : 360° = luas per potong pizza : 1386 cm²

                                                 ^{luas per potong pizza = 1386 cm2 : 6}

                                       ^{luas per potong pizza = 231 cm2} 

 

Sumber:

http://mafia.mafiaol.com/2014/02/hubungan-antara-keliling-dan-luas-lingkaran.html 

http://rumus-matematika.com/cara-menghitung-perubahan-luas-dan-keliling-jika-jari-jari-berubah/ 

http://mardliyahmunfarida.blogspot.co.id/2013/05/hubungan-antara-sudut-pusat-panjang.html 

Rumus Mencari Luas Lingkaran

Rumus Mencari Luas Lingkaran Jika Jari-Jari Diketahui

Jika jari-jari lingkaran diketahui maka rumus untuk mencari luas lingkaran yakni:

L = πr²

Di mana:

L = luas lingkaran

π = 3,14 atau 22/7

r = jari-jari lingkaran

Perlu diketahui, jika jari-jari lingkaran yang diketahui merupakan kelipatan dari 7 maka gunakan π = 22/7, sedangkan jika jari-jari lingkaran yang diketahui merupakan bukan kelipatan dari 7 maka gunakan π = 3,14.

Contoh Soal:

Ali akan membuat kolam ikan yang berbentuk lingkaran dengan jari-jari 7 m. Hitunglah luas kolam ikan yang akan dibuat oleh Ali.

 

Sumber gambar:
meityfarida.wordpress.com

Penyelesaian:

Karena yang diketahui hanya jari-jarinya dan panjang jari-jari lingkaran merupakan kelipatan 7 maka gunkan π = 22/7. Luas lingkaran dapat dihitung yakni:

L = πr²

L = (22/7).(7 m)²

L = 154 m²

Jadi, luas kolam ikan yang akan dibuat oleh Ali adalah 154 m²

Rumus Mencari Luas Lingkaran Jika Diameter Diketahui

Kita ketahui bahwa diameter (garis tengah) lingkaran merupakan dua kali jari-jari lingkaran atau dapat ditulis:

d = 2r <=> r = ½d

Maka rumus mencari luas lingkaran jika diameter diketahui yakni:

L = πr²

L = π(½d)²

L = ¼πd²

Jadi rumus untuk mencari luas lingkaran jika diameter lingkaran diketahui yakni:

L = ¼πd²

Di mana:

L = luas lingkaran

π = 3,14 atau 22/7

d = diameter lingkaran

Contoh soal :

jika diketahui sebuah lingkaran mempunyai diameter 14 cm. Berapakah luas lingkaran tersebut?
Penyelesaian:
Diketahui:
d = 14 cm
karena d = 2 × r maka:
r = d/2
r = 14/2
r = 7 cm
Ditanyakan: Luas lingkaran?
Jawab:
Luas = π × r²
Luas = 22/7 × 7²
Luas = 154 cm²
Jadi, luas lingkaran tersebut adalah 154 cm².

Rumus Mencari Luas Lingkaran Jika Keliling Diketahui

Untuk mencari rumus luas lingkaran jika keliling lingkaran diketahui dapat dilakukan dengan dua cara yakni dengan rumus tidak langsung dan langsung. Untuk rumus tidak langsung Anda harus mencari jari-jari atau diameter lingkaran tersebut kemudian cari luasnya dengan rumus:

L = πr²

atau

L = ¼πd²

Sedangkan untuk mencari rumus langsung perhatikan uraian ini. Sebelum itu Anda harus paham dengan rumus keliling lingkaran. Perlu Anda ketahui bahwa rumus keliling lingkaran yakni:

K = 2πr

Dimana:

          K = keliling lingkaran

          π = 22/7 atau 3,14

          r = jari-jari lingkaran

maka:

r = ½K/π

Dengan mensubstitusi r = ½K/π ke rumus luas lingkaran L = πr², maka:

L = πr²

L = π(½K/π)²

L = ¼ (K²/π)

Jadi rumus mencari luas lingkaran jika keliling lingkaran diketahui adalah:

L = ¼ (K²/π)

Contoh soal:

1. Sebuah lingkaran ingin diketahui seberapa besar luas yang dimilikinya. Kemudian, diketahui bahwa keliling lingkarannya adalah 88 cm. Jika diketahui π = 22/7,

Berapa luasnya??
Diketahui :

• keliling = 88 cm
• π = 22/7

Ditanya :

• luas...??

Jawab :

Keliling = 2πr

---

88 = 2 x ²²/₇ x r
88 = ⁴⁴/₇ x r
r = 88 : ⁴⁴/₇
r = 88 x ⁷/₄₄
r = 14 cm.
Mencari luas lingkaran

---

---

Setelah berhasil menemukan jari-jari (r) dari lingkaran
Maka sekarang adalah giliran untuk mencari luasnya
Luas lingkaran = πr² = π x r x r
Luas lingkaran = ²²/₇ x 14 x 14
Luas lingkaran = 616 cm²

Sumber:
http://mafia.mafiaol.com/2014/09/rumus-mencari-luas-lingkaran.html
https://masfikr.com/rumus-keliling-lingkaran/
https://solusimatematika85.blogspot.co.id/2016/04/mencari-luas-lingkaran-diketahui-keliling.html